Кривизна дуги
Любая дуга — это часть окружности. Соответственно радиус дуги равен радиусу окружности:
Рисунок 542.1. Дуга — часть окружности
На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.
Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.
Понятие кривизны дуги формулируется так:
Кривизна дуги — это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги
Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:
kд. = α/m (542.3)
А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:
m = Rα (542.4)
то, подставив значение длины дуги в уравнение (542.3), получим:
kд. = α/m = α/Rα = 1/R (542.1.2)
Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:
m = ПRα/180 (542.4.1)
но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью
m = ПR360/180 = 2ПR = lокр. (542.4.2)
Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.
И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия — это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:
Рисунок 542.2. Дуга из точки начала координат.
то расстояние между точками — это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х — это стрела дуги h.
Почему линзы следует выбирать индивидуально
Иногда во время ношения линз можно столкнуться с дискомфортом. Это связано с тем, что линзы были подобраны неправильно. В некоторых случаях также может возникнуть значительное ухудшение зрения. Чтобы этого не произошло выбор необходимо делать в зависимости от индивидуальных особенностей глазного яблока.
Во время использования глазных капель может появиться зуд
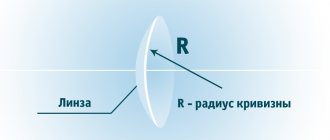
Контактная коррекция зрения обязательно должна осуществляться только в индивидуальном порядке, так как от правильной посадки линзы будет зависеть дальнейший комфорт использования линз. Если радиус кривизны будет отличаться от радиуса роговицы, тогда вы можете столкнуться с дискомфортом.
Радиус кривизны прямой линии
Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.
Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:
ρп.л. = ∞ (542.5)
kп.л = 1/∞ = 0 (542.6)
Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье «Основы геометрии. Определения основных элементов, пятый элемент». Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой — прямой линией конечной длины. Поэтому
все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими
Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:
1. Из уравнения (542.1) можно сделать вывод, что:
kp = 1 (542.7)
Соответственно для прямой линии:
0·∞ = 1 (542.7.2)
Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.
2. Если прямая — это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.
Это означает, что радиусы проведенные в концах дуги — прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке — центре окружности.
Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.
Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.
Такие дела.
Кривизна линз в цифрах
Есть стандартный показатель BC, чаще всего встречающийся у взрослых — 8,6 мм. Он может колебаться в пределах 8,3–9,0 мм. Например, при миопии прозрачная мембрана в передней части глаза становится более выпуклой, а при кератоконусе — приподнимается над глазным яблоком.
Подобрать КЛ в соответствии с BC не трудно, если BS не выходит за установленные границы. При другом BS линзы заказывают индивидуально. Изготавливаются они дольше, но идеально описывают форму роговицы.
Радиус кривизны точки
Точка — это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки — не совсем понятно. Я же считаю, что точка — это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:
ρт. = 0 (542.8)
kт. = 1/0 = ∞ (542.9)
И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.
Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.
Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия «бесконечность». Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность — это даже не постоянная, а переменная величина. Например луч — это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.
Возможным выходом из этой ситуации является принятие понятия «бесконечность», как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия — идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.
И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 — координаты центра окружности), то:
Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.
R2 = x2 + y2 (541.1.2)
А в общем случае, когда координаты центра окружности не совпадают с началом координат:
Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.
R2 = (x — u)2 + (y — v)2 (542.10)
Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых — не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.
Как ее определить?
Самостоятельное определение базовой кривизны роговицы невозможно. Простая примерка линз не даст точного представления о том, каковы ее показатели.
Это связано с тем, что дискомфорт, вызванный неправильным их подбором, может возникнуть далеко не сразу.
Кроме того, неверно выбранные материал и диаметр также дают неприятные ощущения, и невозможно будет понять, что конкретно не так с надетыми линзами, не подходят ли они по кривизне или по какому-то другому признаку.
Поэтому для того, чтобы узнать эту характеристику своих глаз, потребуется помощь офтальмолога.
В первую очередь, необходима процедура рефрактокератометрии, которая покажет параметры роговицы глаза. Она безболезненна и занимает не больше нескольких минут.
Закончив с предварительной диагностикой и получив примерное представление о состоянии и кривизне роговицы, можно примерить линзу и определить плотность ее прилегания к глазу. Для этого после надевания линзы врач проводит осмотр с помощью щелевой лампы.
Для того чтобы убедиться, что линза села на роговицу не слишком сильно, в глаз закапывается флуоресцеин — светящийся под ультрафиолетовой лампой раствор.
По интенсивности и глубине его проникновения под линзу нетрудно понять, правильно ли была подобрана ее кривизна.
Только после этого врач сможет выписать рецепт, в котором будут точно указаны оптическая сила, диаметр и базовая кривизна идеально подходящих линз.
Конечно же, существуют и другие параметры, которые тоже важны при их использовании: это индивидуальная реакция на различные материалы, показатели мягкости и жесткости, однако, они не могут быть выявлены при осмотре и здесь больной должен ориентироваться только на свои ощущения.
Консультация у врача перед покупкой
Очень важно не заниматься самолечением, даже если услуги офтальмолога понесут за собой некоторые затраты. Это можно объяснить тем, что незнающему человеку тяжело будет разобраться в параметрах линз и собственной роговицы.
При плоской посадке (большая линза) осложнения будут не такими серьезными, но при крутой посадке (маленькая линза) последствия станут довольно неприятными: может развиться гипоксия роговицы, кератит и другие инфекционные болезни глаз.
Врач-офтальмолог для установления точных параметров роговицы использует в процессе работы рефрактокератометр. Так, определится базовая кривизна и диаметр роговицы, соответственно, и контактных линз.
Помимо этого, врач обязательно подбирает пробные линзы с необходимыми параметрами, которые можно носить лишь несколько часов или суток. Используя щелевую лампу, офтальмолог определяет степень подвижности линзы на глазу и полученную посадку. Дополнительно можно закапать глаз специальным средством и оценить его распределение под контактной линзой с помощью ультрафиолетового света.